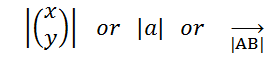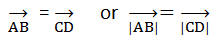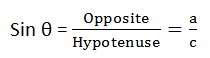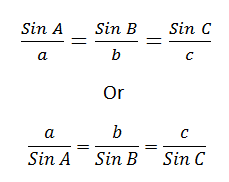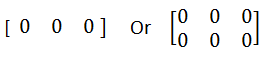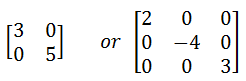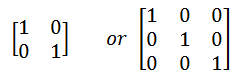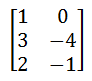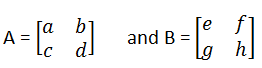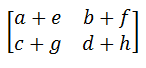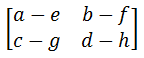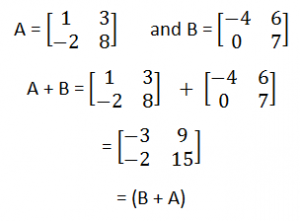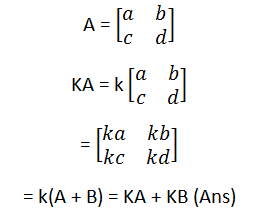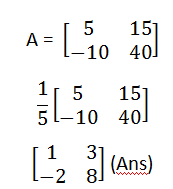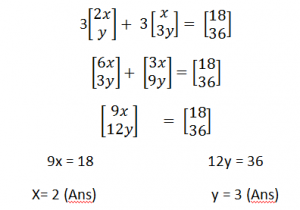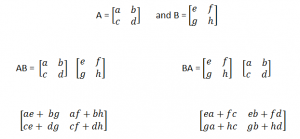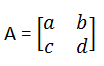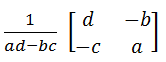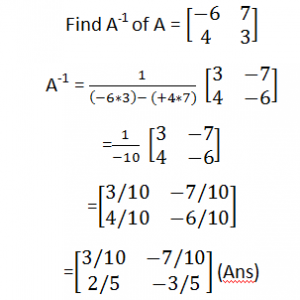PAST PAPERS

For the past papers , click here:
http://papers.xtremepapers.com/index.php?dir=CIE/Cambridge%20International%20O%20Level/Mathematics%20D%20%28Calculator%20Version%29%20%284024%29/

Vectors(In 2 dimensions)

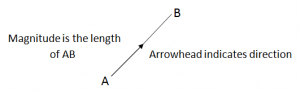
Vectors have both magnitude and direction.

To Denote A Vector as a:

Column Vector:

Resultant Vector:

Single Letter in bold. i.e  a.

Position Vector:

Position vectors are also called as end points.

Magnitude:

To Find the Modulus / Magnitude of a position vector:

Addition And Subtraction of Vectors:

(Parallelogram Law of Addition)

(Triangular Law of Addition) nose to tail

• The negative sign reverses the directionof a vector.
• The result of a-b is a + – b e. subtracting b is equal to adding the negative of b.

Equal Vectors:

If two line segmants AB  and CD are parallel, in same direction and equal in length, then AB and CD are equal vectors.

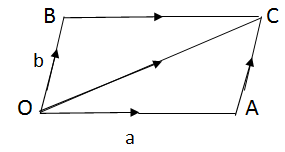
Parallel Vectors:

Vectors are parallel, if they have the same direction.

Both components of one vector must be in the same ratio to the corresponding components of the parallel vector.

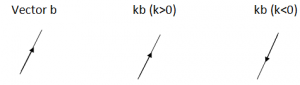
Vector b                        kb (k>0)                         kb (k<0)

If a = kb, the vectors a and b are parallel and are in same direction.

Magnitude of a is

Congurence & Similarity

Congurency:

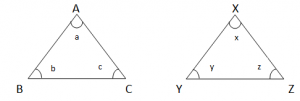
Two geometric figures are congurent, if they are of the same shape and size.

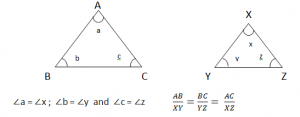
                                                                                 AB =XY               ∠a = ∠x

BC = YZ               ∠b = ∠y

AC = XZ               ∠c = ∠z

Tests of Congurency:

• Side Side Side (SSS) – all sides are equal
• Angle Angle Angle (AAA) – all angles are same
• Side Angle Side (SAS) – two sides and one angle are equal
• Right Angled – Hypotenuse – Side – one right angle and hyp & side equal

≡  – To denote “ is congruent to”

≢ – To denote “ is not congruent to”

Similarity:

When two figures are similar, they are exactl the same in shape but not in size.

Test:

• Equal corresponding Angles:

The angles of one triangle are equal to corresponding angles of the other triangle.

• Proportional Corresponding Angles.
• Two Pairs of Proportional Corresponding Sides with equal angles.

We right similarity as ( ~ ) i.e ΔABC ~ ΔDEF

Ratios of Area And Volumes:

Same Ratio:

Ratio of Area: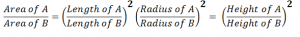

Ratio of Volume: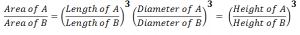

Bearings

The bearing of point B from another point A is:

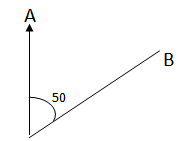
• An angle measured north to at A.
• In a clockwise direction.
• Written as three- figured number (i.e from 000 to 300 degrees).

The bearing of B from A is 050 degree.

Angles Of Elevation and Depression:

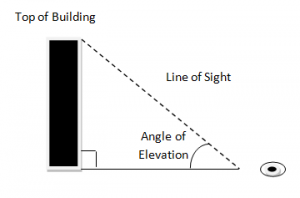
Angle of Elevation:

When a person looks at something above his or her location e.g (The top of a building). The angle formed between the horizontal ground and the line of sight is called the angle of elevation.

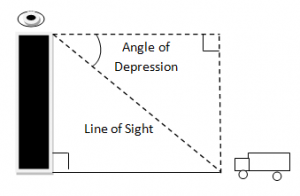
Angle Of Depression:

When a person looks at something below his or her location, the angle between the imaginative horizontal and vertical and the line of sight is the angle of depression.

Angle of depression is always of equal value as angle of depression because they are alternative angles.

Trigonometry

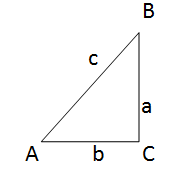
Pythagoras Theoram:

For all the right angled triangles “the square on the hypotenuse (c²) is equal to the sum of all the squares on the other two sides (a² + b² ).

c² = a² + b²

Trigonometrical Ratios of Acute Angle:

All angles in a right angle triangle are acute angles. (between 0 to 90 degrees).

Sine:

Cosine:

Tangent: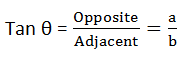

Tip to remember this SOH CAH TOA.

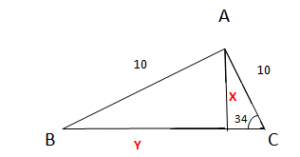
Example:

Q: Find the unknown values of :

           Sin 30 = Opposite / Hypotenuse

Sin 30 = x / 13

X = 6.5 Ans

Y² + X² = 10²

Y² = 10² –  6.5²

Y = 7.60 (Ans)

Trigonometrical Ratios of Obtuse Angles:

The trigonometric ratios of an obtuse angle (between 90 and 180 degree) can be expressed in terms of the adjacent acute angle that lies in the same straight line.

Area of Triangle:

For a known right angled triangle with any two sides given and the area.

 Area = ½ ab sin C

Area = ½ bc sin A

Area = ½ ac sin B

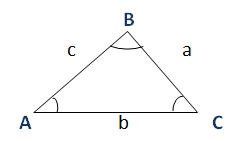
Sine Rule:                

                                           

It can be used when:

• Two angles and one side given.
• Two sides and one non-included angle given.

Cosine Rule:

a²⁼ b² = c² – (2bc cos A)

b²⁼ a² = c² – (2ac cos B)

c²⁼ a² = b² – (2ab cos C)

It can be used when:

• Three sides are given.
• Two sides and one angle is given.

Properties of a circle

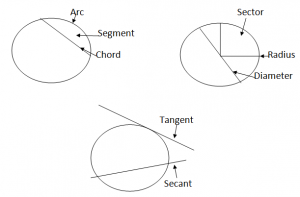
Circle Definitions:

Geometrical Properties of Circle:

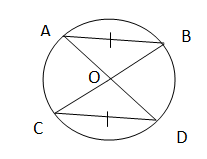
If 2 chords in a circle area congruent, then the 2 angles at the centre of the circle are identical.

AB = CD (Equal Chords)

∠ AOB = ∠ COD

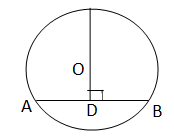
The perpendicular bisector of a chord passes through the centre of a circle

E.g.

AD = DB

∠CDA = ∠CDB

=90°

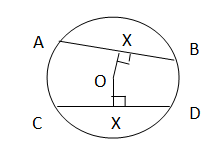
2 congurent chords in a circle are of the same distance from the centre of the circle.

E.g.

AB = CD

OX = OY

Angle Properties Of Cicle:

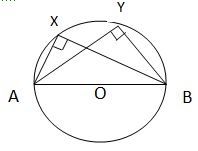
Angle in a semi circle is a right angle.

∠AXB = ∠AYB = 90°

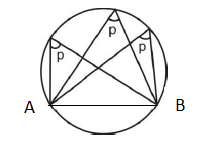
Angles in the same segment are equal

∠p = ∠p = ∠p

Matrices

In Mathematics, matrices are arrays of numbers arranged in rows and columns.

Types of Matrices:

Row Matrix:

Coloumn Matrix:

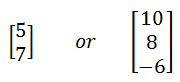
Special Matrix:

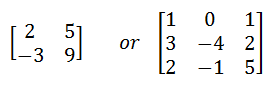
Null Matrix (0):

Null Matrix is that matrix, that only contains number 0 in it.

Diagonal Matrix:

Also known as square matrix, in which all element zero except the diagonal upper left to lower left.

Identity (or unit) Matrix (I):

The elements in the diagonal are one’s only.

Writing the order of Matrices:

Order = Number of Rows *  Number of Columns

Example:

Order = 3*2

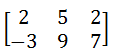
Order = 2 * 3

Addition and Subtraction of Matrices:

Matrices of the same order are added (or subtracted) by adding (or subtracting)  the corresponding elements in each matrix.

Adding A + B:                     Subtracting A – B:

 

Rules:

A+B = B+A : A and B can change position when adding.

(A+B) + C = A + (B+C): order of operation bracket first.

A – B ≠ B –A:  A and B should not change positions when subtracting.

Example:

Scaler Multiplication of a Matrix by a real number:

Example:

Equal Matrix:

If two matrices A and B are of the same order and their corresponding elements are equal, then A = B.

Example:

Multiplication of Two or More Matrices:

Matrices can only be multiplied only if they are compatible. They are compatible when the number of rows of the second matrix is the same as the number of coloumns of the first matrix.

Rules:

AB ≠ BA : A and B should not change positions

(AB)C = A(BC): If 3 or more matrices you can choose whichever 2 to    multiply first.

Example:

Inverse Of Matrix:

Determinant A  = ad – bc

A^{-1 =} 

Remember:

• If Determinant = 0 then the matrix has no inverse.
• Multipying by the inverse of the inverse of a matrix gives the same result as dividing by the matrix.

E.g.

If AB = C

A^-1AB = A^-1C

B= A^–1C

Example of Inverse of Matrix:

• If Determinant = 0 then matrix has no inverse.
• Multipying by the inverse of the inverse of a matrix gives the same result as dividing by the matrix.

E.g.